时间序列问题的特征工程

注意

本指南重点介绍单表时间序列问题的特征工程；它不涵盖如何处理用于其他机器学习问题类型的时间性多表数据。关于在 Featuretools 中处理时间的更通用指南可以在此处找到。

时间序列预测包括使用较早的观测值预测目标的未来值。在用于时间序列问题的数据集中，数据具有固有的时间顺序（由时间索引确定），并且我们正在预测的顺序目标值彼此高度依赖。时间序列问题的特征工程利用了这样一个事实：较近期的观测值比距离较远的观测值更具预测性。

本指南将探讨如何使用 Featuretools 自动进行单变量时间序列问题的特征工程，即仅包含时间索引和目标列的问题。

我们将使用一个包含一个 DataFrame 的温度演示 EntitySet，该 DataFrame 名为 temperatures。temperatures dataframe 包含我们将预测的每日最低温度。总共有三列：id、Temp 和 Date。id 列是 Featuretools 所必需的索引。另外两列对于单变量时间序列问题很重要：Date 是我们的时间索引，Temp 是我们的目标列。工程特征将从这两列构建。

es = load_weather()

es["temperatures"].head(10)

Downloading data ...

	id	Date	Temp
0	0	1981-01-01	20.7
1	1	1981-01-02	17.9
2	2	1981-01-03	18.8
3	3	1981-01-04	14.6
4	4	1981-01-05	15.8
5	5	1981-01-06	15.8
6	6	1981-01-07	15.8
7	7	1981-01-08	17.4
8	8	1981-01-09	21.8
9	9	1981-01-10	20.0

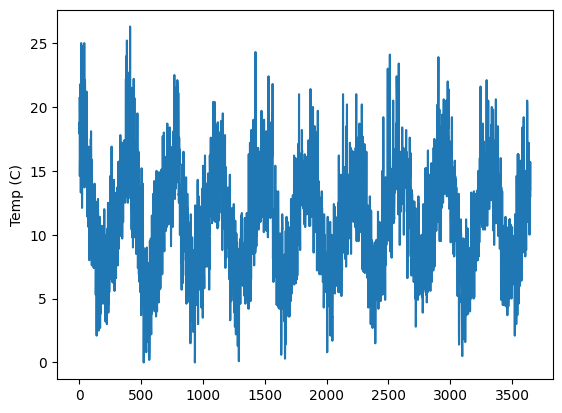
es["temperatures"]["Temp"].plot(ylabel="Temp (C)")

<Axes: ylabel='Temp (C)'>

理解特征工程窗口

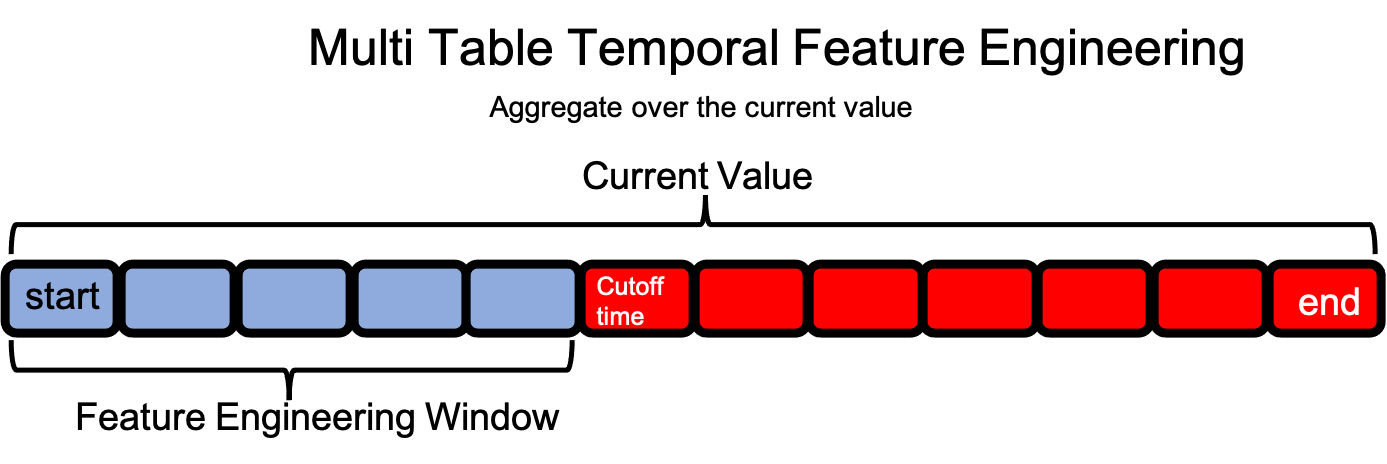
在多表数据集中，目标 DataFrame 中单行数据的特征工程窗口从时间索引开始向前扩展，覆盖子 DataFrame 中的观测值，直到达到截止时间或最后一个时间索引。

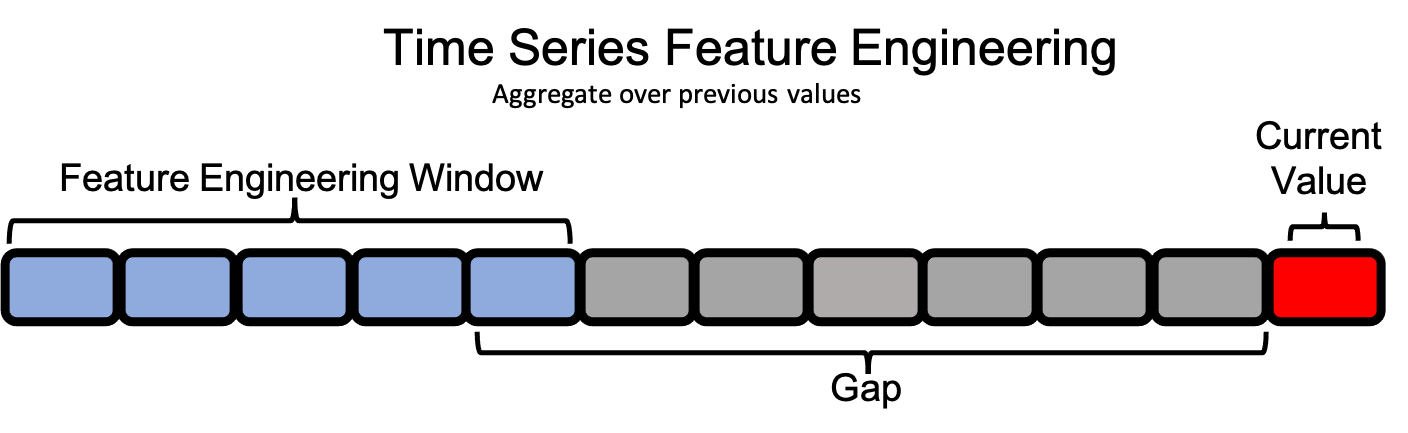
在单表时间序列数据集中，单个值的特征工程窗口在同一列中向后扩展。因此，截止时间和最后一个时间索引的概念不再以同样的方式相关。

例如：单表时间序列数据集的截止时间会创建训练集和测试集的数据分割。在 DFS 过程中，截止时间之后不会计算特征。通常情况下，在创建 EntitySet 之前分割数据可以更简单地实现相同的行为，因为在计算特征矩阵时过滤数据比提前分割数据计算量更大。

split_point = int(df.shape[0]*.7)

training_data = df[:split_point]
test_data = df[split_point:]

因此，由于我们无法使用现有参数定义每个观测值的特征工程窗口，我们需要定义新的概念：gap 和 window_length。这些概念将允许我们设置一个存在于每个观测值之前的特征工程窗口。

间隔和窗口长度

请注意，在定义间隔和窗口长度时，我们将使用整数。这意味着我们的数据以均匀间隔出现——在本例中是每天——所以数字 n 对应于 n 天。对非均匀间隔的支持正在进行中，可以通过 Woodwork 方法 df.ww.infer_temporal_frequencies 进行探索。

如果我们在时间点 t，我们可以访问早于 t 的时间点的信息（过去的值），并且我们无法访问晚于 t 的时间点的信息（未来的值）。那么，我们在特征工程方面的限制将来自于我们能精确地访问到 t 之前何时的数据。

考虑一个例子，我们记录需要一周才能摄取的数据；我们能访问到的最早数据是七天前的，即 t - 7。我们将这称为我们的 gap。一个 gap 为 0 的情况将包含当前实例本身，这在时间序列问题中必须小心避免，因为它会暴露我们的目标。

我们还需要确定在 t - 7 之前我们可以回溯多远。回溯太远可能会失去近期观测值的预测力，但回溯太近可能无法捕捉到数据所显示的所有行为。在此示例中，假设我们每次只想查看 5 天的数据。我们将这称为我们的 window_length。

gap = 7
window_length = 5

设置了这两个参数（gap 和 window_length）后，我们就定义了特征工程窗口。现在，我们可以继续定义我们的特征原始特征。

时间序列原始特征

对于时间序列问题，我们将重点关注三种类型的原始特征。其中一种将从时间索引中提取特征，另外两种将从我们的目标列中提取特征。

日期时间转换原始特征

我们需要一种方法将时间体现在我们的时间序列特征中。是的，使用近期温度对于预测未来温度具有极高的预测性，但也有大量历史数据表明一年中的月份是室外温度的一个很好的指标。然而，如果我们查看数据，会发现尽管日期变化，但观测值总是在同一小时获取，因此 Hour 原始特征可能不会很有用。当然，在以小时或更精细频率测量的数据集中，Hour 可能会非常具有预测性。

datetime_primitives = ["Day", "Year", "Weekday", "Month"]

日期时间转换原始特征的完整列表可以在此处查看。

延迟原始特征

对目标列最简单的事情是构建目标列的延迟（或滞后）版本的特征。我们将在特征工程窗口中为每个观测值创建一个特征，因此我们将在时间范围从 t - gap - window_length 到 t - gap 进行遍历。

为之，我们可以使用我们的 Lag 原始特征，并为窗口中的每个实例创建一个原始特征。

delaying_primitives = [Lag(periods=i + gap) for i in range(window_length)]

滚动转换原始特征

由于我们可以访问整个特征工程窗口，我们可以对该窗口进行聚合。Featuretools 有几种滚动原始特征可以实现这一点。在此，我们将使用 RollingMean 和 RollingMin 原始特征，并相应地设置 gap 和 window_length。在这里，间隔 (gap) 非常重要，因为当间隔为零时，意味着当前观测值的目标值存在于窗口中，这将暴露我们的目标。

对于引用数据框中较早值的其他原始特征，也存在这种担忧。因此，在使用原始特征进行时间序列特征工程时，必须非常小心，不要在计算特征值时使用包含当前观测值的目标列上的原始特征。

rolling_mean_primitive = RollingMean(
    window_length=window_length, gap=gap, min_periods=window_length
)

rolling_min_primitive = RollingMin(
    window_length=window_length, gap=gap, min_periods=window_length
)

滚动转换原始特征的完整列表可以在此处查看。

运行 DFS

现在我们已经定义了时间序列原始特征，我们可以将它们传入 DFS 并获得特征矩阵！

让我们看看上面我们用 gap 和 window_length 定义的实际特征工程窗口。下面是一个示例，展示了如何在不暴露目标值的情况下，使用相同的特征工程窗口提取多个特征。

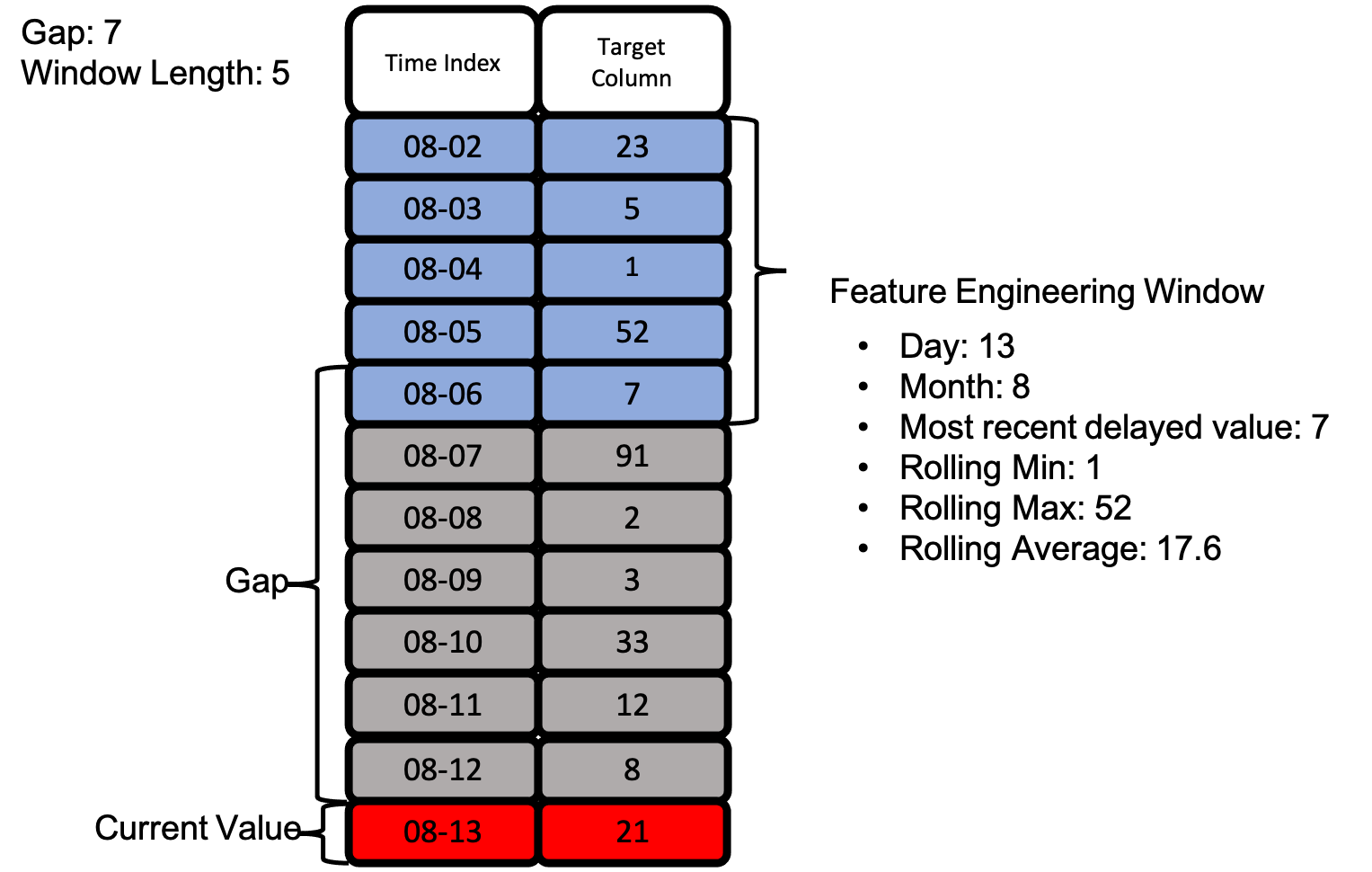
通过上图，我们看到我们定义的所有原始特征如何被用来仅从我们能访问的两列数据创建多个特征。

fm, f = ft.dfs(
    entityset=es,
    target_dataframe_name="temperatures",
    trans_primitives=(
        datetime_primitives
        + delaying_primitives
        + [rolling_mean_primitive, rolling_min_primitive]
    ),
    cutoff_time=pd.Timestamp("1987-1-30"),
)

f

[<Feature: Temp>,
 <Feature: DAY(Date)>,
 <Feature: LAG(Temp, Date, periods=10)>,
 <Feature: LAG(Temp, Date, periods=11)>,
 <Feature: LAG(Temp, Date, periods=7)>,
 <Feature: LAG(Temp, Date, periods=8)>,
 <Feature: LAG(Temp, Date, periods=9)>,
 <Feature: MONTH(Date)>,
 <Feature: ROLLING_MEAN(Date, Temp, window_length=5, gap=7, min_periods=5)>,
 <Feature: ROLLING_MIN(Date, Temp, window_length=5, gap=7, min_periods=5)>,
 <Feature: WEEKDAY(Date)>,
 <Feature: YEAR(Date)>]

fm.iloc[:, [0, 2, 6, 7, 8, 9]].head(15)

	Temp	LAG(Temp, Date, periods=10)	LAG(Temp, Date, periods=9)	MONTH(Date)	ROLLING_MEAN(Date, Temp, window_length=5, gap=7, min_periods=5)	ROLLING_MIN(Date, Temp, window_length=5, gap=7, min_periods=5)
id
0	20.7	NaN	NaN	1	NaN	NaN
1	17.9	NaN	NaN	1	NaN	NaN
2	18.8	NaN	NaN	1	NaN	NaN
3	14.6	NaN	NaN	1	NaN	NaN
4	15.8	NaN	NaN	1	NaN	NaN
5	15.8	NaN	NaN	1	NaN	NaN
6	15.8	NaN	NaN	1	NaN	NaN
7	17.4	NaN	NaN	1	NaN	NaN
8	21.8	NaN	NaN	1	NaN	NaN
9	20.0	NaN	20.7	1	NaN	NaN
10	16.2	20.7	17.9	1	NaN	NaN
11	13.3	17.9	18.8	1	17.56	14.6
12	16.7	18.8	14.6	1	16.58	14.6
13	21.5	14.6	15.8	1	16.16	14.6
14	25.0	15.8	15.8	1	15.88	14.6

上面是我们的时间序列特征矩阵！滚动和延迟特征是从我们的目标列构建的，但并未暴露它。我们现在可以使用特征矩阵来创建机器学习模型，以预测未来的每日最低温度。